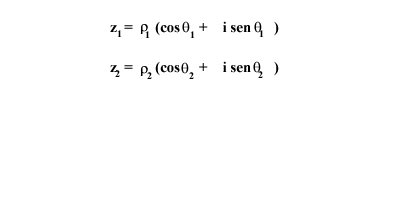VOLTAR
Quantas vezes, ao calcularmos o valor de Delta (b2- 4ac) na resolu��o da equa��o do 2� grau, nos deparamos com um valor negativo (Delta < 0).
Nesse caso, sempre dizemos ser imposs�vel a raiz no universo considerado (normalmente no conjunto dos reais- R). A partir da�, v�rios matem�ticos estudaram este problema, sendo Gauss e Argand os que realmente conseguiram expor uma interpreta��o geom�trica num outro conjunto de n�meros, chamado de n�meros complexos, que representamos por C.
N�meros Complexos
Chama-se conjunto dos n�meros complexos, e representa-se por C, o conjunto de pares ordenados, ou seja:
z = (x,y)
onde x pertence a R e y pertence a R.
Ent�o, por defini��o, se z = (x,y) = (x,0) + (y,0)(0,1) onde i=(0,1), podemos escrever que:
z=(x,y)=x+yi
Exemplos:
(5,3)=5+3i
(2,1)=2+i
(-1,3)=-1+3i ...
Dessa forma, todo o n�meros complexo z=(x,y) pode ser escrito na forma z=x+yi, conhecido como forma alg�brica, onde temos:
x=Re(z, parte real de z
y=Im(z), parte imagin�ria de z
Igualdade entre n�meros complexos
Dois n�meros complexos s�o iguais se, e somente se, apresentam simultaneamente iguais a parte real e a parte imagin�ria. Assim, se z1=a+bi e z2=c+di, temos que:
z1=z2<==> a=c e b=d
Adi��o de n�meros complexos
Para somarmos dois n�meros complexos basta somarmos, separadamente, as partes reais e imagin�rias desses n�meros. Assim, se z=a+bi e z2=c+di, temos que:
z1+z2=(a+c) + (b+d)
Subtra��o de n�meros complexos
Para subtrairmos dois n�meros complexos basta subtrairmos, separadamente, as partes reais e imagin�rias desses n�meros. Assim, se z=a+bi e z2=c+di, temos que:
z1-z2=(a-c) + (b-d)
Pot�ncias de i
Se, por defini��o, temos que i = - (-1)1/2, ent�o:
i0 = 1
i1 = i
i2 = -1
i3 = i2.i = -1.i = -i
i4 = i2.i2=-1.-1=1
i5 = i4. 1=1.i= i
i6 = i5. i =i.i=i2=-1
i7 = i6. i =(-1).i=-i ......
Observamos que no desenvolvimento de in (n pertencente a N, com n variando, os valores repetem-se de 4 em 4 unidades. Desta forma, para calcularmos in basta calcularmos ir onde r � o resto da divis�o de n por 4.
Exemplo:
i63 => 63 / 4 d� resto 3, logo i63=i3=-i
Multiplica��o de n�meros complexos
Para multiplicarmos dois n�meros complexos basta efetuarmos a multiplicac�o dois dois bin�mios, observando os valores das pot�ncia de i. Assim, se z1=a+bi e z2=c+di, temos que:
z1.z2 = a.c + adi + bci + bdi2
z1.z2= a.c + bdi2 = adi + bci
z1.z2= (ac - bd) + (ad + bc)i
Observar que : i2= -1
Conjugado de um n�mero complexo
Dado z=a+bi, define-se como conjugado de z (representa-se por z-) ==> z-= a-bi
Exemplo:
z=3 - 5i ==> z- = 3 + 5i
z = 7i ==> z- = - 7i
z = 3 ==> z- = 3
Divis�o de n�meros complexos
Para dividirmos dois n�meros complexos basta multiplicarmos o numerador e o denominador pelo conjugado do denominador. Assim, se z1= a + bi e z2= c + di, temos que:
z1 / z2 = [z1.z2-] / [z2z2-] = [ (a+bi)(c-di) ] / [ (c+di)(c-di) ]
M�dulo de um n�mero complexo
Dado z = a+bi, chama-se m�dulo de z ==> | z | = (a2+b2)1/2, conhecido como ro
Interpreta��o geom�trica
Como dissemos, no in�cio, a interpreta��o geom�trica dos n�meros complexos � que deu o impulso para o seu estudo. Assim, representamos o complexo z = a+bi da seguinte maneira

Exercícios Resolvidos
1 - Sejam os complexos
z1=(2x+1) + yi e z2=-y + 2i
Determine
x e
y de modo que z
1 + z
2 = 0
Temos que:
z
1 + z
2 = (2x + 1 -y) + (y +2) = 0
logo, é preciso que:
2x+1 - y =0 e y+2 = 0
Resolvendo, temos que
y = -2 e x = -3/2
2 - Determine
x, de modo que
z = (x+2i)(1+i) seja imaginário puro
Efetuando a multiplicação, temos que:
z = x + (x+2)i + 2i
2
z= (x-2) + (x+2)i
Para z ser imaginário puro é necessário que (x-2)=0, logo
x=2
3 - Qual é o conjugado de
z = (2+i) / (7-3i)?
Efetuando a divisão, temos que:
z = (2+i) / (7-3i) . (7+3i) / (7+3i) = (11 + 3i) / 58
O conjugado de Z seria, então
z- = 11/58 - 13i/58
4 - Os módulos de
z1 = x + 201/2i e
z2= (x-2) + 6i são iguais, qual o valor de
x?
Então, |z
1= (x
2 + 20)
1/2 = |z
2 = [(x-2)
2 + 36}
1/2
Em decorrência,
x
2 + 20 = x
2 - 4x + 4 + 36
20 = -4x + 40
4x = 20, logo
x=5
5 - Escreva na forma trigonométrica o complexo
z = (1+i) / i
Efetuando-se a divisão, temos:
z = [(1+i). -i] / -i
2 = (-i -i
2) = 1 - i
Para a forma trigonométrica, temos que:
r = (1 + 1)
1/2 = 2
1/2
sen t = -1/2
1/2 = - 2
1/2 / 2
cos t = 1 / 2
1/2 = 2
1/2 / 2
Pelos valores do seno e cosseno, verificamos que t = 315º
Lembrando que a forma trigonométrica é dada por:
z = r(cos t + i sen t), temos que:
z = 21/2 ( cos 315º + i sen 315º )
Exercícios propostos
1 - Calcule o valor de
(1 + i)8
Resposta:
16
2 - Calcule as raízes quartas de
-8 + 8 31/2i
Resposta:
31/2 + i , -31/2 - i , 1 - 31/2i, -1 + 31/2i
3 - Qual o valor de
m para que o produto
(2+mi)(3+i) seja um imaginário puro ?
Resposta:
8
4 - Sendo
z1 = 5(cos 60º + isen 60º) e
z2 = 3(cos 30º + i sen 30º), qual é o valor de z
1 . z
2 ?
Resposta:
8i
5 - Qual o valor do determinante da matriz
A = (z2z zz) onde
z = cos 135º + i sen 135º?
Resposta:
i