| Probabilidade (resumo) |
| Definições |
| Probabilidade |
| Exercícios resolvidos |
| Exercícios propostos |
Embora o cálculo de probabilidades seja uma ferramenta indispensável ao estudo da Estatística e em muitos modelos da Pesquisa Operacional, seus conceitos e aplicabilidade são ensinados cada vez mais no Ensino Médio
Normalmente é no ensino da Análise Combinatória que começa a se estabelecer os conceitos e as noções básicas para a compreensão do cálculo de probabilidades. Entretanto, quase sempre, não é dada a continuidade a este estudo, bastante importante no nosso dia-a-dia
, o que provoca o esquecimento deste tipo de cálculo, por parte dos alunos
Devido a isto, segue um resumo da teoria e alguns exercícios resolvidos e a resolver, a fim de que os alunos possam tirar suas dúvidas, quando necessário.
Sejam algumas definições essenciais
1) Experiência ( experimento) aleatório
Toda a experiência repetida em condições idênticas em que aparecem resultados distintos é dita
experiência aleatória
Exemplo
o lançamento de uma moeda, de um dado, a extração de bolas de uma urna, ...
2) Espaço amostral (ou das probabilidades)
É como se chama o conjunto de todos os resultados possíveis de um experimento
Exemplo:
O espaço amostral do lançamento de um dado é de ter 6 (seis) faces diferentes voltadas para o lançador.
3) Evento
No conjunto do espaço amostral, qualquer dos seus subconjuntos é chamado de evento.
Exemplo:
No lançamento de um dado a ocorrência de termos um número ímpar na face virada é um evento, ou seja:
A = {1,2,3,4,5,6} (espaço amostral)
E = {1,3,5} (evento)
Repare que E é subconjunto de A
Obs:
Evento certo : se A = E
Evento impossível : se E = Ø (vazio)
Evento elementar : n(E) = 1 (só existe um elemento)
4) Evento complementar
É o evento que ocorre, se e somente se o outro evento não ocorrer
Obs:
1. A interseção de 2 eventos complementares é vazia
2. A união de 2 eventos complementares é o espaço amostral
Probabilidade
Seja o espaço amostral
A = { a1, a2, a3, ..., ak }
Associemos a cada ponto amostral um número real p { ai } ou pi chamado de probabilidade do evento { ai }, ou probabilidade de ocorrência do ponto amostral ai, tal que:
1) 0 £ pi £ 1
2) p1 + p2 + p3 + ... + pk = 1
Define-se então como probabilidade do evento E a relação entre o número de elementos do referido evento e o número de elementos do espaço amostral, ou seja:
p(E) = n(E) / n(A)
Exemplo:
Qual a probabilidade no lançamento de um dado, da face voltada para cima ser um número menor que 4 ?
Temos que:
E = {1,2,3} --> n(E) = 3
A = {1,2,3,4,5,6} --> n(A) = 6
Logo:
p(E) = 3 / 6 = 1/2
Conceitos e propriedades das probabilidades
União de 2 eventos
Neste caso, temos que observar um pouco a teoria dos conjuntos para facilitar a compreensão. Seja, portanto, a figura abaixo:
Pela teoria dos conjunto, temos que:
n(XÈY) = n(X) + n(Y) - n(XÇY)
Pela definição de probabilidade, temos que:
n(XÈY) / n(A) = [ n(X) + n(Y) - n(XÇY) ] / n(A)
ou ainda
n(XÈY) / n(A) = n(X)/n(A) + n(Y)/n(A) - n(XÇY)/n(A)
ou seja
p(XÈY) = p(X) + p(Y) - p(XÇY)
Exemplo:
Uma urna contem 30 bolas numeradas de 1 a 30. Uma bola é extraida ao acaso. Qual a probabilidade desta ser múltiplo de 5 e 6 ?
Temos que:
X : múltiplo de 5 --> X = {5,10,15,20,25,30}
Y : múltiplo de 6 --> Y = {6,12,18,24,30}
Então:
p(X) = 6/30 = 1/5
p(Y) = 5/30 = 1/6
p(XÇY) = 1/30
Então:
p(XÈY) = 1/5 + 1/6 - 1/30 = 10/30 = 1/3
Teorema da probabilidade total
Independência de dois eventos
Dado 2 eventos X e Y de um espaço amostral A, diremos que X independe de Y se
p(X|Y) = p(X)
isto é, X independe de Y se a ocorrência de X não afeta a probabilidade de Y
Obs
Se X independe de Y então Y independe de X
ou seja
Se p(X|Y) = p(X) então p(Y|X) = p(Y)
Neste caso, então
p(XÇY) = p(X) . p(Y)
Exemplo:
Dois praticantes de tiro ao alvo, A e B, apresentam a seguinte probabilidade de acertar o alvo:
p(A) = 1/3 e p(B) = 2/3
Como A e B são independentes, qual a probabilidade de A e B acertarem o alvo ?
Como p(AÇB) = p(A) . p(B)
Então
p(AÇB) = 1/3 . 2/3 = 2/9
Obs
Generalizando a propriedade, temos que:
p(E1ÇE2 ... ÇEn) = p(E1) . p(E2) . ... .p(En)
Lei Binomial da Probabilidade (Bernoulli)
Seja uma sequência de experimentos independentes, isto é, a probabilidade de um resultado independe do outro. Se em cada experimento puder ocorrer dois resultados, um chamado de "sucesso" e o outro de "fracasso" caracterizamos os experimentos de Bernoulli
Para este tipo de experimento, onde:
p = sucesso e q = fracasso
Se tivermos os eventos
E1 : ocorre sucesso no experimento Xi, ou seja p(Xi) = p
E2 : ocorre fracasso no experimento Xic, ou seja p(Xic) = q
podemos, neste caso, empregar a lei binomial para o cálculo da probabilidade, ou seja
pk = Cn,k . pk . qn-k
Exemplo:
Numa cidade 10% das pessoas possuem carro da marca X. Se 30 pessoas são selecionadas ao acaso, com reposição, qual a probabilidade de exatamente 5 pessoas possuirem carro da marca X ?
Seja:
sucesso : a pessoa tem carro da marca X
fracasso : a pessoa Não tem carro da marca X
Então
p = 0,1 ; q = 0,9 ; n = 30
Aplicando a lei binomial, temos
pk = C30,5 . 0,15 . 0,925 @ = 0,102
Exercícios Resolvidos
1.Dois dados são lançados simultaneamente. Qual é a probabilidade de se obter a soma dos pontos igual a 8 ou dois números iguais ?
2.Uma urna contem x bolas brancas e 3x bolas pretas e 3 bolas vermelhas. Uma bola é extraída ao acaso. Determine o menor valor possível de x a fim de que a probabilidade de a bola ser sorteada ser preta seja maior que 70%.
Pelos dados temos que:
3x / (4x + 3) > 0,7
resolvendo temos que
0,2x > 2,1 ou seja x > 10,5
Como x deve ser inteiro logo x = 11
3. Uma urna tem 3 bolas brancas e duas pretas. Extraindo-se 2 bolas simultaneamente, calcule a probabilidade de serem uma de cada cor.
O espaço amostral é: C5,2 = 10
Como temos 2 bolas pretas e 3 brancas o total de ocorrências para uma de cada cor será:
2 x 3 = 6
A probabilidade será então 6/10 ou seja 3/5
4. Se no problema anterior as bolas fossem retiradas uma a uma com reposição, qual seria a nova probabilidade?
Neste caso seriam eventos independentes, logo teríamos que somar as suas probabilidades
Então, teriamos
Se primeiro branca e depois preta : p(E1) = 3/5 . 2/5 = 6/5
Se primeiro preta e depois branca : p(E2) = 2/5 . 3/5 = 6/5
A probabilidade total seria então 12/25
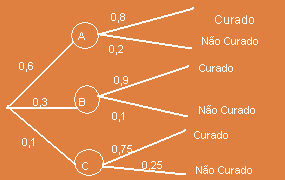
5. Uma clinica especializada trata de 3 tipos de moléstias: A, B e C. 60% dos que procuram a clínica são portadores da moléstia A, 30% são portadores de B e 10% de C. As probabilidades de cada moléstia nesta clinica são, respectivamente, 0,8 ; 0,9 ; 0,75. Um doente sai curado da clinica. Qual a probabilidade de que ele sofresse da molésta B?
Pelos dados podemos representar conforme figura abaixo

6. Uma moeda é lançada 8 vezes. Qual a probabilidade de observarmos, no máximo, 3 caras?
Então, temos :
n = 8 ( número de vezes)
p = 1/2 (probabilidade de dar cara)
q = 1/2 (probabilidade de não dar cara)
Usando a lei binomial podemos ter:
p0 = C8,0.(1/2)0.(1/2)8 = 1/256
p1 = C8,1.(1/2)1.(1/2)7 = 8/256
p2 = C8,2.(1/2)2.(1/2)6 = 28/256
p3 = C8,3.(1/2)3.(1/2)5 = 56/256
Então:
p = 93 / 256 = 0,36
Exercícios Propostos
1. De um grupo de 200 pessoas, 160 tem fator Rh positivo, 100 tem o tipo O e 80 tem fator Rh positivo e tipo O. Se uma dessas pessoas for selecionada ao acaso, qual a probabilidade de acontecer:
a) ter seu sangue com fator Rh positivo?
b) seu sangue não ser do tipo O?
Resp. a) 4/5 e b) 1/2
2. Um grupo é constituido por 8 homens e 6 mulheres. Quatro pessoas são selecionadas ao acaso, sem reposição. Qual a probabilidade de que ao menos duas sejam homens ?
Resp. 0,825
3. Jogando-se tres dados, qual a probabilidade de que a soma dos pontos obtidos seja superior a 15?
Resp. 0,046
4. A probabilidade de um guarda aplicar quatro ou mais multas em um dia é de 64%. A probabilidade de aplicar quatro ou menos multas em um dia é de 56%. Qual a probabilidade dele aplicar exatamente quatro multas?
Resp. 0,20
6. A probabilidade de um satélite ser recuperado com algum aproveitamento é de 1/10. Se tres satélites são lançados, qual a probabilidade de se recuperar apenas um satélite?
Resp. 0,243