Devido à facilidade da compreensão visual, que são inerentes no estudo da Geometria, muitas verificações são realizadas através de processos indutivos.
Assim, muitos demonstrações são feitas aproveitando-se bastante a característica visual dos elementos geométricos analisados.

Podemos exemplificar algumas dessas verificações de verdades geométricas, utilizando alguns textos do livro "Aprendendo e Ensinando Geometria de Lindiquist, M.M. & Shulti, A.P. - Ed. Atual

a) aplicação do teorema de Pitágoras

Seja o quadrado com as medidas assinaladas (lado = a+b), formando um novo quadrado em seu interior.
A área do quadrado inicial é dada por:
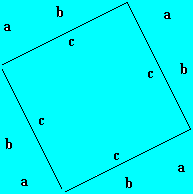
S = ( a + b )²
A área do quadrado interno é dada por:
S^' = c²

Na decomposição da figura, é fácil verificar que contornando o quadrado interno temos 4 triângulos, cuja área de cada um é dada por:
S^'' = a . b / 2
Então, a soma de todos os elementos geométricos no interior do quadrado nos dá:
S^' + 4S^'' = c² + 2ab
Ora, mas isto nada mais é do que o valor da área do quadrado original. Então, podemos deduzir que
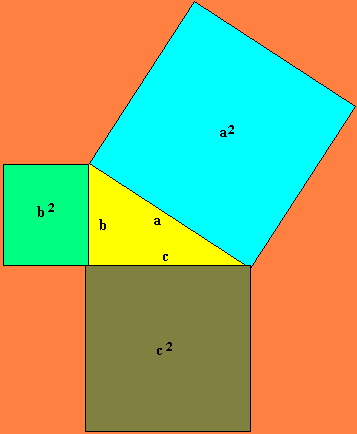
( a + b ) ² = c² + 2ab
Desenvolvendo o produto notável temos que:
a² + 2ab + b² = c² + 2ab
O que, finalmente, nos induz ao raciocínio de Pitágoras, ou seja: a² + b² = c²

Geometricamente mostra-se tal afirmação na famosa figura abaixo:
b) Soma dos ângulos externos de um polígono

Vamos começar desenhando um triângulo e explicitando seus ângulos externos. Assim, temos: Pela formação de ângulos suplementares na figura, temos :
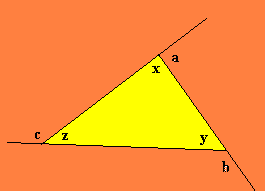
a + x = 180º
b + y = 180º
c + z = 180º
Somamdo-se, membro a membro, temos que:
a + b + c + x + y + z = 3 . 180º
Como x + y + z = 180º, então:
a + b + c + 180º = 3 . 180º
logo,
a + b + c + = 360º
Vamos agora verificar o que acontece se o polígono tiver 4 lados
Então:
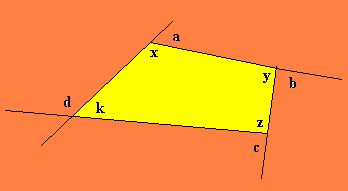
a + x = 180º
b + y = 180º
c + z = 180º
d + k = 180
Somando-se, membro a membro, temos:
a + b + c + d + x + y + z + k = 4 . 180º
Como x + y + z + k = 2 . 180º, temos:
a + b + c + d + 2 . 180º = 4 . 180º
Então: a + b + c + d = 360º
Ainda não satisfeito deste processo de indução, vanos tentar agora um polígono de 5 lados:
Então
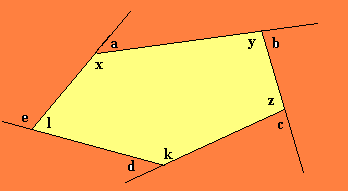
a + x = 180º
b + y = 180º
c + z = 180º
d + k = 180
e + l = 180º
Somando-se, temos:
a + b + c + d + e + x + y + z + k + l = 5 . 180º
Como x + y + z + k + l= 3 . 180º, temos:
a + b + c + d + e + 3 . 180º = 5 . 180º
Então: a + b + c + d + e= 360º
Verifica-se, por indução que a soma dos ângulos externos de um polígono convexo será sempre igual a 360 graus.

c) a soma dos números inteiros consecutivos e positivos

Mais uma vez a geometria com o seu apelo visual nos ajuda a descobrir verdades algébricas.
Queremos, então descobrir a soma de:
1 + 2 + 3 + 4 + .... + n
Explorando a caracteristica visual da geometria, podemos ter a figura abaixo:
A área da parte hachurada, que representa a soma desejada, nada mais é do que a metade da áres do retângulo, logo:
1 + 2 + 3 + 4 + .... + n = [n(n+1)] / 2
que confere com o que já sabemos da álgebra, quando calculamos a soma de uma progressão aritmética finita.

d)verificação do cálculo de probabilidades

A facilidade de enxergarmos a solução de um problema, através de uma figura, tem ajudado muito no emprego da geometria na compreensão de problemas relativos à pesquisa operacional e ao cálculo de probabilidades. Como exemplo deste último, seja o problema a seguir:

Problema:
Seja E um ponto médio do segmento AB. Escolhe-se C aleatoriamente em AE e D em EB. Qual a probabilidade de CD < 1/4 AB ?

Como estamos falando de probabilidade, estabeleçamos um sistema de coordenadas AB, de modo que a coordenada A seja 0 e a coordenada B seja 1. Sejam x e y, respectivamente, as coordenadas de C e D. Assim, temos:
As condições do problema exigem que:
0 < x < 1/2 e 1/2 < y < 1
O gráfico do conjunto de pares ordenados (x,y) que verificam essas condições é o interior do quadrado FGHI, na figura:
Como CD = y - x e AB = 1, a condição CD < 1/4 AB é equivalente a:
y - x < 1/4
A condição y - x < 1/4 (abaixo da reta) obriga que o par (x,y) esteja no interior do triângulo JIK
Levando-se em conta que a área do triângulo JIK é 1/8 da área do quadrado FGHI (verificar na figura), podemos afirmar que a probabilidade procurada é 1/8.

Esses são apenas alguns exemplos de como, visualmente, a geometria nos ajuda na solução de problemas