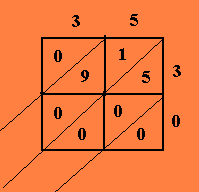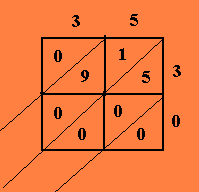Hoje em dia, é muito simples realizar a operação de multiplicação. Entretanto, os matemáticos já a conheciam muito antes do surgimento do famoso sinal de vezes (x)
Imagine, então, como deveria se proceder a operação sem o conhecimento das regras que atualmente utilizamos.

A título de curiosidade vamos destacar dois métodos utilizados pelos antigos matemáticos.

Método dos escribas egípcios

Para multiplicar os egípcios usavam tabelas que eram construídas dobrando-se os valores de acordo com número de parcelas usadas. Uma vez a tabela pronta para determinado fator, os resultados correspondentes eram somados para se obter o valor da multiplicação.
Exemplo: Seja a multiplicação 35 vezes 30
Criamos, então, a tabela do fator 30

Linha	Parcelas	Resultado
1	1	30
2	2	60
3	4	120
4	8	240
5	16	480
6	32	960
...	...	...

Para formar 35 parcelas basta somarmos as parcelas das linhas 1, 2 e 6. Logo o resultado de 35 x 30 será a soma dos resultados das linhas 1, 2 e 6, ou seja 35 x 30 = 30 + 60 + 960 = 1050
Outro exemplo: 41 vezes 19 vezes 14

Vamos construir a tabela do fator 19

Linha	Parcelas	Resultado
1	1	19
2	2	38
3	4	76
4	8	152
5	16	304
6	32	608
...	...	...

Para formar 41 usamos as linhas 1, 4 e 6
Então
41 x 19 = 19 + 152 + 608 = 779
Agora, temos que multiplicar 779 vezes 14
Vamos construir a tabela do fator 14

Linha	Parcelas	Resultado
1	1	14
2	2	28
3	4	56
4	8	112
5	16	224
6	32	448
7	64	896
8	128	1792
9	256	3584
10	512	7168
...	...	...

Para obtermos 779, devemos usar as linhas 1, 2, 4, 9 e 10
Então:
779 x 14 = 14 + 28 + 112 + 3584 + 7168 = 10906

Apesar de trabalhoso, porque obriga a criação de várias tabelas do fator multiplicador, é bastante curioso e interessante o método utilizado pelos antigos egípcios.

Metodo da Gelosia (veneziana)

Este método tem este nome por ter semelhança com um tipo de janela muito comum nas ruas de Veneza, cidade da Itália.
Os fatores da multiplicação eram separados para cada veneziana (representada por um quadrado e sua diagonal) e os resultados parciais de mesma direção de cada veneziana eram somados para o resultado final

Exemplo: Seja o caso anterior 35 vezes 30
Construamos as venezianas ( 4 quadrados: 2 para o fator 35 e 2 para o fator 30)

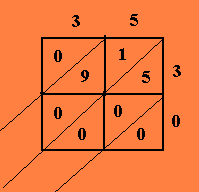No prolongamento de cada diagonal do quadrado, temos os resultados (algarismos) parciais que devemos somá-los e dispô-los em ordem.
Assim, temos:
0, 0+9+1,0+0+5 ou seja 0, 10, 5, 0
Passando a segunda parcela para a ordem superior, temos
1, 0, 5, 0 logo 35 x 30 = 1050

Seja o outro exemplo dado 41 vezes 19 vezes 14
Façamos primeiro a operação 41 vezes 19
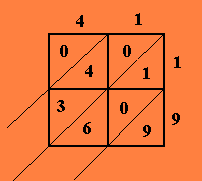Da veneziana, temos
0,3+4+0,6+0+1,9 ou seja 0,7,7,9, portanto 41 x 19 = 779
Agora vamos montar a veneziana de 779 vezes 14
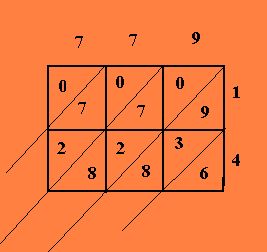Da veneziana, temos
0,0+7+2,0+7+2+8,9+3+8,6 ou seja 0,9,17,20,6
Passando unidades da 2º para a 3º ordem, temos: 0,9,19,0,6
Passando unidades da 3º para a 4º ordem, temos: 0,10,9,0,6
Passando unidades da 4º para a 5º ordem, temos: 1,0,9,0,6
Logo 41 x 19 x 14 = 10906

Neste caso, diferente dos egípcios, esses matemáticos já tinham maior conhecimento do sistema de numeração decimal, porém não conheciam o nosso famoso sinal de vezes(x) e as nossas regras atuais de multiplicação

É interessante observar a engenhosidade dos matemáticos antigos para realizar as operações básicas da matemática, Muito devemos a eles o nosso estado atual de evolução nos cálculos matemáticos.