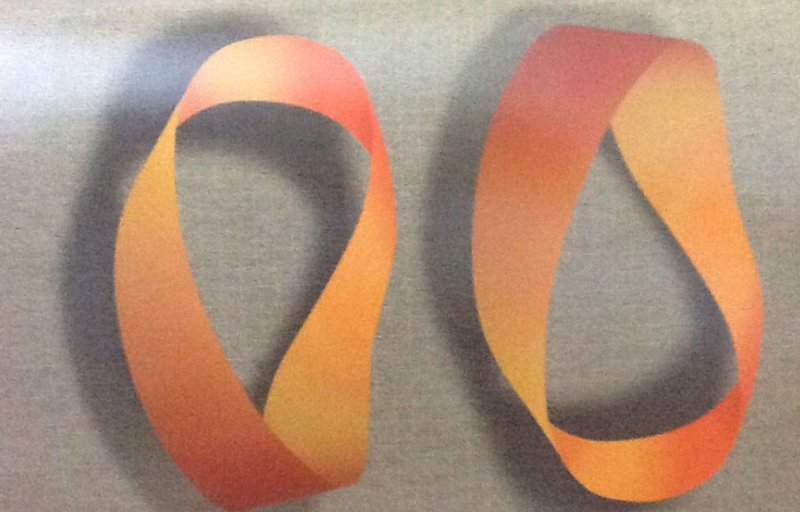CURIOSIDADES MATEMÁTICAS

TRIÂNGULO DE PASCAL

Como continua a sequência ? (1,1),(1,2,1),(1,3,3,1),(1,4,6,4,1), ....

Este é um importante problema da álgebra. Comece a desenvolver (1+x):
(1+x)²= 1 + 2x + 1x²
(1+x)³= 1 + 3x + 3x² + 1x³
(1+x)⁴= 1 + 4x + 6x² + 4x³ + 1x⁴
A próxima seria:
(1+x)⁵= 1 + ?x + ?x² + ?x³ + ?x⁴ + 1x⁵
que poderíamos desenvolver como :
(1+x)⁵= C_5,0 + C_5,1x + C_5,2x² + C_5,3x³ + C_5,4x⁴ + C_5,5s⁵
ou seja:
(1+x)⁵= 1 + 5x + 10x² + 10x³ + 5x⁴ + 1x
que daria a sequencia :(1,5,10,10,5,1).

Poderíamos continuar, infinitamente, mas Blaise Pascal procurou uma maneira de encontrar a sequencia de forma mais rápida. Daí surgiu a construçãodo famoso Triângulo de Pascal, conforme figura abaixo:

TEOREMA DE BAYES

Suponha que um teste para uma determinada doença tenha a precisão de 90%
Suponha, agora, uma pessoa escolhida aleatoriamente, tenha feito o teste e deu positivo. Qual a probabilidade de que ele tenha, realmente a doença.?
Você precisa saber a probabilidade anterior de uma pessoa escolhida, aleatoriamente, ter a doença.

Suponhamos que 1% da população esteja doente.

O teorema de Bayes nos diz como encontrar a probabilidade de se ter a doença no teste positivo.
No caso, por exemplo, em um grupo de 1000 pessoas, cerca de 10 tem a doença (1%) e o teste de 9 delas dará positivo ("verdadeiros positivos")
As 990 restantes não teem a doença e 10% delas, 99 pessoas, farão testes que darão positivo ("falsos positivos").

Os falsos positivos superam o número de verdadeiros positivos em 99 a 9, de modo que a chance da pessoa escolhida ter a doença é de 1 para 11.

O que Bayes tenta demonstrar são questões filosóficas sobre a própria natureza da probabilidade. Em particular, a aparição de probabilidades anteriores sugere que não há sentido em atribuir probabilidade a eventos sem antes utilizar testes reiterados para determinar a frequência do evento.

A FITA DE MOBIUS

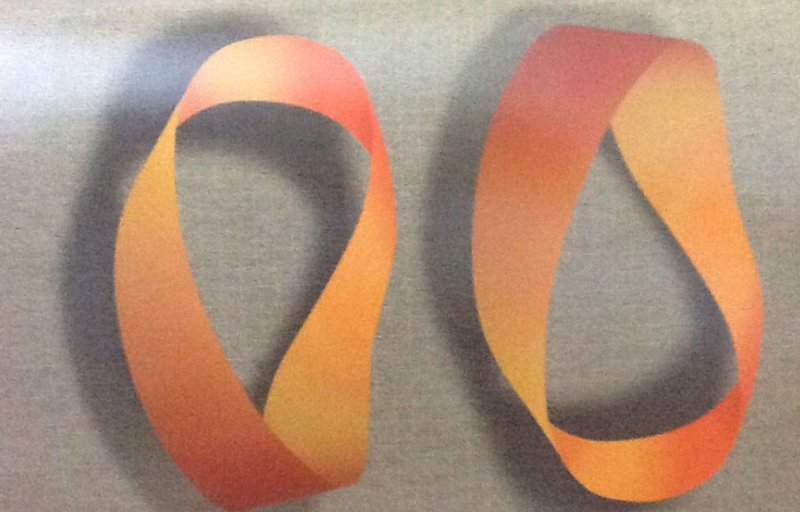
Comece com uma fita de papel retangular. Se você colar uma ponta na outra, isso vai produzir um anel comum, cilindrico. Mas, se fizer um meio giro na fita, obterá algo mais instigante: uma fita de Mobius.

O que é interessante nessa simples faixa de papel é que ela tem apenas um lado e uma borda. Se você começar a traçar uma linha ao longo do centro da fita, ela vai cruzar tanto o lado de dentro como o de fora antes de reencontrar o seu começo, uma vez que os dois lados são, na realidade, o mesmo.

Você pode estar se perguntando sobre o que aconteceria se fizesse um corte ao longo desta linha central. Na verdade, cortar a fita não produz duas novas voltas, mas apenas uma. Tente e veja!

As fitas de August Mobius fascinaram crianças e adultos, desde que eles as descobriu, em 1858. Mas, para os matemáticos, a importância das fitas reside em outros formatos que podem ser construídos a partir delas.

Se você pegar duas fitas de Mobius e colá-las uma na outra, ao longo de suas bordas, vai produzir uma superfície de um só lado, conhecida como a Garrafa de Klein. O único problema é que é impossível fazer isso no espaço tridimensional, sem que a superfície da garrafa atravesse a si mesma.
O estranho anel torcido de Mobius, com um lado só, é o passaporte para um mundo de formatos exóticos.

GEOMETRIA DE ORIGAMI

O origami, secular arte japonesa de dobrar papel, é intrinsicamente geométrico.

Nas últimas décadas, a matemática do origami sofreu numerosos avanços. Huzita, Justin e Hatoru formularam um conjunto de axiomas para esta arte , de forma parecida com aquela pela qual os axiomas geométricos foram formulados.
Além disso, teoremas matemáticos que abordam questões teóricas sobre o origami foram provados nos últimos anos.

Algorítmos que ajudam a encontrar soluções ótimas para a dobratura de figuras complexas foram desenvolvidos por Lang e outros, juntamente com programas de computador que os utilizam. Desse modo, é possível produzir padrões de vincos que indicam as dobras necessárias e, o sentido que devem ser feitas, para se obter a forma desejada.

Enquanto o origami se concentrou tradicionalmente na criação de formas que representam animais e plantas, o objetivo primário de algumas técnicas modernas dessa arte são as formas geométricas.
Nos mosaicos de origami, uma grade de vincos é usada como ponto de partida na criação de formas geométricas, que frequentemente envolvem repetições. Shuzo Fujimoto é amplamente reconhecido como o iniciador desta vertente.

No origami modular, múltiplos módulos geométricos, cada um deles composto de uma única folha de papel, são combinados para formar modelos mais complexos.

A matemática do origami tem sido usada para lidar com vários problemas de engenharia do mundo real. Como exemplo, técnicas do origami teem sido usadas para determinar a forma ideal de dobar um airbag, de modo que seja acionado corretamente numa colisão automobilística.
Outro exemplo, um "stent", inspirado no origami, foi desenvolvido para alargar artérias e veias obstruídas. Muitos outros exemplos existem em nosso mundo tecnológico.

O CUBO MÁGICO

O cubo mágico foi criado por Erno Rubick, em 1974 e comercializado em seu país natal, a Hungria, a partir de 1977. Em 1980, a Ideal Toy Company adquiriu os direitos do invento, e hoje, já foramvendidos mais de 300 milhões de unidade ao redor do mundo.

Um mecanismo de pivô permite, que cada uma das seis faces do cubo seja rodada de forma independente. Existem mais de 43 quintilhões ( 10 ¹⁸) de arranjos possíveis das 27 peças. A solução do cubo se torna mais fácil pela memorização dos algorítmos que produzem certos resultados desejados, tais como o de alterar as cores de três cantos sem produzir nenhuma outra mudança.

Uma notação de movimentos desenvolvida por David Singmaster permite que os algorítmos seja registrados por escrito. Singmaster também desenvolveu uma das soluções gerais mais populares para o quebra-cabeça.

Para os matemáticos, o cubo é nada mais que a manifestação física de um grupo algébrico. Dessa perspectiva, sua análise mostra que ele pode ser solucionado a partir de qualquer posição inicial, em não mais de 20 movimentos. Apenas em 2010, foi obtida uma prova matemática desse resultado.
O record mundial (meados de 2013) de solução do cubo pertence a Mats Valk, com um tempo menor que 6 segundos. Mas a "corrida do cubo" admite variações, como os desafios de resolvê-lo de olhos vendados, usando uma única mão e até mesmo com os pés.

Além do cubo 3x3, existem cubos 2x2, 5x5, 6x6, 7x7. O número de permutações do cubo 7x7 ultrapassa 10 ¹⁵⁹, ou seja, 1 seguido de 160 zeros.
Existem também versões baseadas no tetraedro, no octaedro, no dodecaedro e no icosaedro.

O MAPA DE QUATRO CORES

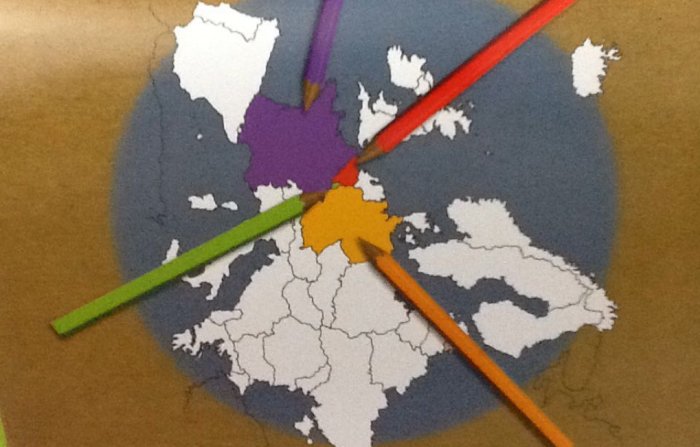
Se num mapa, você decide que dois países vizinhos não podem compartilhar a mesma cor, o que é normal, temos o problema do mapa de quatro cores
Por exemplo, países vizinhos como França, Bélgica, Alemanha e Luxemburgo vão exigir cores diferentes. Dessa forma, serão necessárias, ao menos, quatro cores diferentes. Será que, em algum momento, você será obrigado a usar uma quinta cor ? O teorema das quatro cores afirma que não.

Independente do tamanho e da complexidade do mapa que deseja colorir, desde que cada país seja uma região contínua, é possível colorir os países com quatro cores apenas.

Apesar de um enunciado simples, o teorema das quatro cores é extremamente difícil de ser provado. Somente cem anos após proposto pela primeira vez, os matemáticos Kenneth Appel e Wolfgang Haken encontraram uma prova para o teorema.

Enquanto quatro cores são suficientes para colorir mapas em uma esfera ou em um plano, não bastam para mapas em outros tipos de superfície. Fabricantes de mapas que querem colorir um toro ( toro de objeto ) precisam até sete cores, ao passo que um mapa numa fita de Mobius precisa de seis cores.