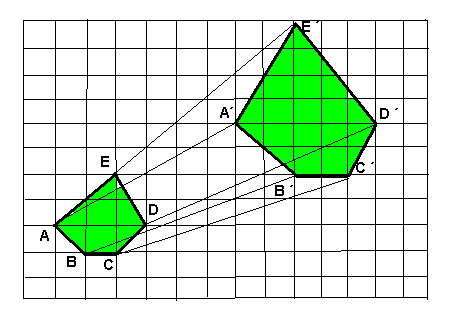
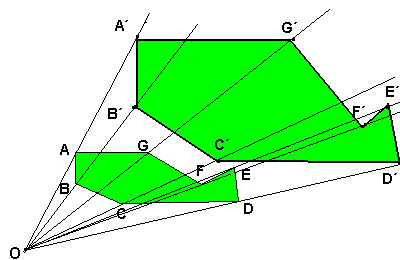
Uma longa aplicação da matemática em nosso dia-a-dia se constitui na semelhança de polígonos. É através da semelhança de diversas figuras poligonais que montamos as conhecidas escalas, seja para ampliação ou redução de tamanho da figura (objeto) original. Um exemplo de ampliação poderia ser o caso de aumentarmos o tamanho de uma peça a fim de estudarmos as possíveis falhas desta peça, em conjunto com outras peças, para formarmos um componente industrial com um índice de falhas dentro dos padrões de mercado. 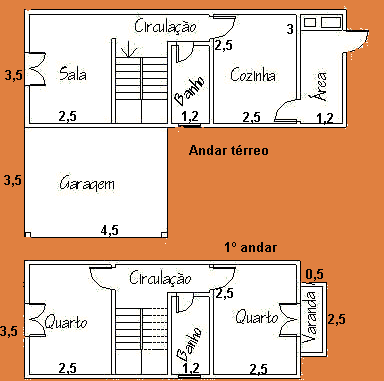Um exemplo de redução poderia ser o caso de uma planta baixa de determinado local para o estudo e análise das obras que deverão ser realizadas naquele local. Muitos outros exemplos poderiam ser citados.

Vamos recordar um pouco sobre o que vem a ser "escala"e dar alguns exemplos práticos para mostrar como é importante o seu conhecimento em nosso cotidiano.


Seja a figura ABCD. Projetemos respectivamente ABCD para A'B'C'D'.
Na figura A'B'C'D', devido ao paralelismo adotado na projeção das figuras , temos que:

AB / A'B' = BD / B'D' = DC / D'C' = CA / C'A' = k

onde k é a razão de proporcionalidade ou semelhança.

Assim, se por exemplo AB tem 5cm de comprimento e A'B' tem 10cm de comprimento, dizemos que:

AB / A'B' = 5 / 10 = 1 / 2 = k

Ou seja, o desenho original tem os seus lados medindo, respectivamente, a metade do desenho projetado. Neste caso, dizemos ser de 1 para 2 a escala adotada.
O desenho obtido é uma figura semelhante ao desenho original, segundo determinada razão de semelhança (k). Na prática, quando expressamos esta razão de forma que o numerador seja a unidade teremos, então, o que chamamos de "escala".

Desta forma, podemos dizer que em uma representação gráfica

Se
D = tamanho real
d = tamanho desenhado
E = denominador da escala
temos que
d / D = 1 / E

Assim, em um mapa geográfico em que 1cm do desenho equivale a 1km na situação real, podemos dizer que a escala é de 1/100000, já que 1km = 100000cm.

A título de ilustração vamos resolver dois exercícios práticos:

1) Dada a planta baixa a seguir, e sabendo-se que a escala é de 1/200, em cm, qual a medida real dos comodos da casa ?


Como a escala � de 1/200cm ou 1/2m, significa que cada unidade equivale a 2metros, assim temos:
Salas : 7 x 5 = 35 m²
Banheiros : 2,4 x 5 = 12 m²
Cozinha : 7 x 5 = 35m²
�rea : 2,4 x 6 = 14,4m²
Garagem : 9 x 7 = 63m²
Quartos : 7 x 5 = 35m²
Varanda : 1 x 5 = 5m²

2) Dado o mapa geográfico a seguir, e sabendo-se que está na escala 1/300, em km, qual a distância da cidade localizada no RJ ao Distrito Federal ?


Verificamos que na escala fornecida cada unidade da mesma (cerca de 1cm) vale 300km. Como no mapa vemos que a reta tra�ada � de pouco mais de 3cms, podemos dizer que a distancia � de aproximadamente 1000km.

Formas de amplia��o e redu��o

Uma forma bem simples de se ampliar ou reduzir figuras é usar papel reticulado como no exemplo abaixo:


� facil verificar que no espa�o reticulado na figura menor a unidade utilizada foi de um "retangulo" e na figura ampliada a unidade utilizada foi de 2 ret�ngulos.

Outra forma é fazer uma projeção cônica, da seguinte maneia:
1) Dada a figura, escolhemos um ponto qualquer O, por exemplo:


2) Ligamos este ponto O à vários pontos extremos da figura prolongando-os


3) Medimos a distância desses pontos e obtemos novos pontos multiplicando respectivamente cada medida por uma constante k (razão de semelhança)


4) Ligamos os novos pontos e temos, neste caso, a ampliação desejada da figura original.


OBS: O ponto O, pode estar em qualquer posição, inclusive no interior da figura.

Como se vê a noção de escala está bastante "entranhada" no nosso dia-a-dia, daí é importante o seu conhecimento.

Se voc� tiver algum bom exemplo de aplica��o da matem�tica, e que ache ser interessante envie-me, e publicarei neste site a sua contribui��o identificada

VOLTAR