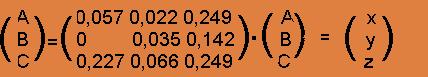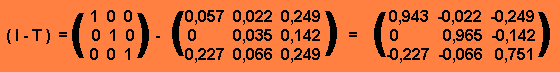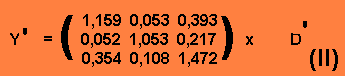Uma das aplicações práticas da notação matricial é o seu uso nas relações insumo-produto usadas no planejamento econômico Na análise de insumo-produto, criada por Wassily Leontief, a economia de um país é dividida em setores e o fluxo dos bens e serviços entre os setores é registrado para indicar as relações entre eles. Desta forma, por exemplo, podemos analisar o PNB (Produto Nacional Bruto) de um país.

Com as tabelas insumo-produto, mostrando o inter-relacionamento entre os diversos setores da economia, podemos analisar os setores que precisam de investimento para almejarmos determinado nível de produção.
A tabela a seguir mostra o inter-relacionamento de alguns setores de um país hipotético. A tabela mostra os valores em milhoes de reais (R$):

	Atividades Intermediárias			Sub- Total	Demanda Final						Total
	A	B	C		D	E	F	G	H	I
A	5	5	70	80	0	4	4	10	80	90	88
B	0	8	40	48	0	2	3	250	20	96	227
C	20	15	70	105	20	13	25	200	18	100	281
V	63	199	101
T	88	227	281

onde:
A - Indústria Extrativa B - Indústria Leve C - Indústria Pesada V - Valor Adicionado T - Total D - Investimento E - Estoques F - Governo G - Consumo Final H - Exportações I - Importações

Por esta tabela, o PNB dos setores deste país seria :
PNB = 63 + 199 + 101 = 363 milhões de reais
Vamos reescrever a tabela mostrando a soma dos destinos da produção:

	Demanda Intermediária		Demanda Final		Produção Total
A =	5 + 5 + 70	+	8	=	88
B =	0 + 8 + 40	+	179	=	227
C =	20 + 15 + 70	+	176	=	281

Fazendo x = 8, y = 179 e z = 176 poderemos fazer análises com a demanda final. Assim temos:

	Demanda Intermediária		Demanda Final
A =	5 + 5 + 70	+	x
B =	0 + 8 + 40	+	y
C =	20 + 15 + 70	+	z

Sabendo que A = 88, B = 227 e C = 281, podemos reescrever a tabela anterior da seguinte maneira:

	Demanda Intermediária		Demanda Final
A =	0,057A + 0,022B + 0,249C	+	x
B =	0 + 0,035B + 0,142C	+	y
C =	0,227A + 0,066B + 0,249C	+	z

Agora, vamos usar o nosso conhecimento de matrizes e reescrever a tabela usando a notação matricial:



que pode ser escrito sob a forma:

Y = TY + D
onde:
Y = matriz de produção total por setor
T = matriz de coeficientes técnicos da demanda intermediária
D = matriz da demanda final
Como serão feitas análises da demanda final, vamos explicitá-la da produção. Assim, temos:
Y = TY + D ou Y -TY = D ou Y(I -T) = D
onde I é a matriz identidade
finalmente, temos:

Y = ( I - T )^-1 . D

Com esta notação matricial poderemos fazer vários estudos da demanda.
Exemplo
Imaginemos que é desejada um demanda final D^´. Pergunta-se: qual deve ser a produção de cada setor para se alcançar a demanda D^´ desejada ?

Na realidade, queremos achar Y^´ tal que:

Y^´ = ( I - T )^-1 . D^´ (I)

Para dar um sentido prático à equação (I), vamos usar os dados do nosso país hipotético.

Em primeiro lugar, vamos calcular ( I - T ).



Agora, vamos calcular ( I - T )^-1

Uma das formas de calcular ( I - T )^-1 é construir uma matriz na qual cada elemento é o da adjunta de ( I - T ), dividido pelo determinante de ( I - T ).

Então, vamos em primeiro lugar, calcular o determinante de ( I - T )

det (I-T) = -(0,022x0,142x0,227) + (0,943x0,965x0,751) - (0,227x0,965x0,249) - (0,943x0,066x0,142)
det (I-T) = -0,001 + 0,683 - 0,055 - 0,009 = 0,618
Como det (I-T) > 0 logo (I-T)^-1 existe.

Agora vamos calcular a matriz dos co-fatores

(0,725 - 0,009)	- (-0,032)	(0,219)
-(-0,017 - 0,016)	(0,708 - 0,057)	- (-0,062 - 0,005)
(0,003 + 0,240)	- (-0,134)	(0,910)

ou seja

0,716	0,032	0,219
0,033	0,651	0,067
0,243	0,134	0,910

Agora, vamos transpor esta matriz para obtermos a matriz adjunta

0,716	0,033	0,243
0,032	0,651	0,134
0,219	0,067	0,910

Finalmente, dividamos cada elemento da matriz adjunta pelo valor do determinante já calculado e vamos obter a matriz inversa (I-T)^-1 desejada

1,159	0,053	0,393
0,052	1,053	0,217
0,354	0,108	1,472

Então, podemos agora reescrever (I) de forma a se fazer as análises desejadas em nosso país hipotético. Assim, temos:



Vamos supor, então, que queremos uma demanda final para a Indústria Extrativa (x) = 10, a Indústria Leve (y) = 180 e a Indústria Pesada (z) = 200.
Qual seria a produção da Indústria Pesada (C) para esse nível de demanda ?

Usando (II), teríamos:

C = 0,354x10 + 0,108x180 + 1,472x200 = 317,380
ou seja, a produção da indústria pesada deveria aumentar em cerca de 36 milhões de reais (317 - 281), se se mantivesse a mesma estrutura tecnológica da economia, representada pela nossa matriz inversa.

Na realidade, para a aplicação prática das matrizes no planejamento econômico, que deseja-se demonstrar, bastaria citar, como exemplo, a equação matricial (II).
Entretanto, foi feito todo um desenvolvimento até chegarmos a equação II de forma a se recapitular o desenvolvimento do cálculo matricial, reconhecido por muitos alunos como um assunto um pouco complexo.