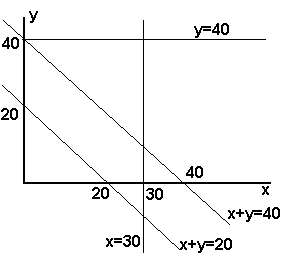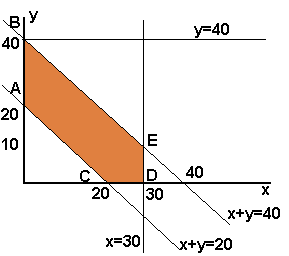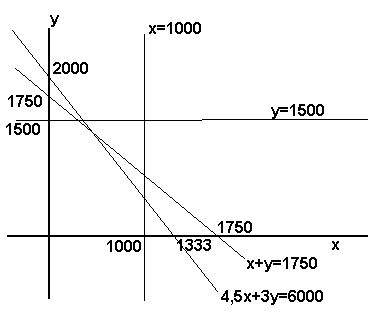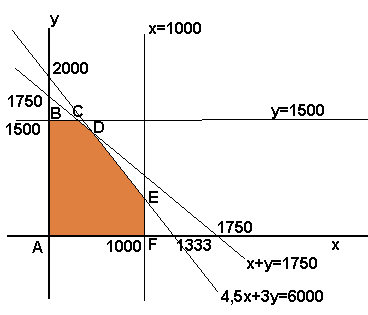Como um bom exemplo do que estamos falando, podemos começar citando o problemas de uma empresa de transporte.

A referida empresa tem 40 unidades de mercadorias no depósito D₁ e 50 unidades no depósito D₂. Precisa enviar 30 unidades ao cliente A e 40 ao cliente B.
Os gastos de transporte por unidade de mercadoria estão indicadas no esquema abaixo:

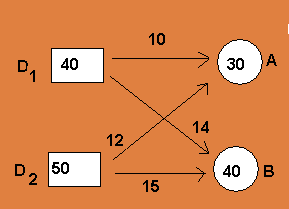
De que maneira deve enviar essas mercadorias para que o gasto com o transporte seja o menor possível ?

Solução

Seja:
x = quantidade que deve enviar a A do depósito D₁
y = quantidade que deve enviar a B do depósito D₁
Então:
30-x = quantidade que deve enviar a A do depósito D₂
40-y = quantidade que deve enviar a B do depósito D₂
A função que representa o gasto G de transporte (função objetiva) é dada por:
G = 10x + 14y + 12(30-x) + 15(40-y)
G = 10x + 14y + 360 - 12x + 600 - 15y
G = -2x - y + 960
Então a função que queremos minimizar é : G = 960 - 2x - y (I)

Agora, vamos às restrições que são as contingências de transporte e da natureza das mercadorias.
a) x>=0 e y>=0 (porque são unidades de mercadorias)
b) x=<30 e y=<40 (porque são as quantidades máximas de entrega nos clientes)
c)x+y =<40 (porque só há 40 unidades em D₁)
d)(30-x)+(40-y)=<50, ou melhor x+y>=20 ( porque só há 50 unidades no depósito D₂ )
Para este problema a solução gráfica é bastante adequada. Então, neste caso, precisaremos traçar as 6 retas correspondentes às restrições citadas, a saber:
x>=0
y>=0
x=<30
x=<40
x+y=<40
x+y>=20
Como x>=0 e y>=0 representamos pelos eixos das abcissas e ordenadas, respectivamente, temos o gráfico de estudo.

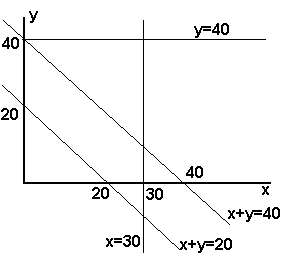
Observando as restrições temos como valores válidos para a função dos gastos G, a área demarcada pelos vértices A(0,20), B(0,40), C(20,0), D(30,0) e E(30,10), conforme a figura abaixo:

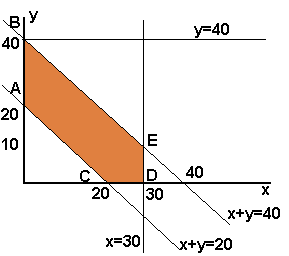
Substituindo-se essas coordenadas dos vértices na função objetiva (I), temos:

Vértice	Valor de G
A(0,20)	940
B(0,40)	920
C(20,0)	920
D(30,0)	900
E(30,10)	890

Como se vê, o menor gasto possível se dá com 890 unidades, o que equivale a dizer que, neste caso, x = 30 e y = 10
Então a solução otimizada nos é dada por:
1) enviar 30 unidades de D₁ a A e 10 unidades de D₁ a B
2) enviar 0 (zero) unidades de D₂ a A (30-x=30-30) e 30 unidades de D₂ a B(40-y=40-10)

Seja agora um exemplo de maximiza��o

Um investidor dispondo de R$ 6000,00 pretende comprar dois tipos de a��es:
Tipo 1- pre�o unit�rio de R$4,50 para compra e rentabilidade anual esperada de 700/9% ;
Tipo 2- pre�o unit�rio de R$3,00 para compra e rentabilidade anual esperada de 100/3% .
Supondo-se que o investidor n�o queira comprar mais de 1750 a��es, e que seu corretor s� poder� comprar at� 1000 a��es do tipo 1 e at� 1500 a��es do tipo 2, que quantidade deve comprar de cada tipo, de forma a obter o m�ximo de capital no final de um ano ?

Solu��o

Usando racioc�nio semelhante ao exemplo anterior, temos que:
x = a��es do tipo 1 a serem compradas
y = a��es do tipo 2 a serem compradas
Sendo M o montante esperado ao final de um ano, deseja-se maximizar, portanto:
M = 4,5(1 + 7/9) x + 3(1 + 1/3)y
ou melhor
M = 8x + 4y (II) que � a fun��o objetiva a ser maximizada.

Agora, vamos verificar as restri��es do investidor
x =<1000 (o corretor s� pode comprar at� 1000 a��es do tipo 1)
y=<1500 (o corretor s� pode comprar at� 1500 a��es do tipo 2)
x + y =< 1750 (o investidor s� quer comprar at� 1750 a��es)
4,5x + 3y =< 6000 (o investidor s� disp�e de R$6000,00)
Al�m destas restri��es existem as restri��es normais de natureza das a��es, ou seja, � imposs�vel falarmos de um n�mero negativo de a��es. Logo, devemos tamb�m ter: x>=0 e y>=0

Para montarmos, de novo, a solu��o gr�fica � necess�rio explicitarmos todas as equa��es lineares existentes das restri��es. Ent�o temos:
x>=0
y>=0
x=<1000
y=<1500
x+y=<1750
4,5x+3y=<6000
Representando estas restri��es no sistema cartesiano, temos;

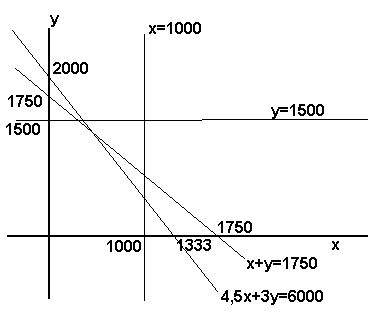
A �rea que atende a todas as restri��es � demarcada pelos v�rtices A(0, 0), B(0, 1500), C(250, 1500), D(500, 1250), E(1000, 500) e F(1000, 0), conforme figura abaixo:

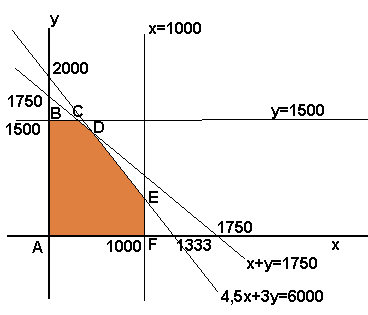
Substituindo estas coordenadas dos v�rtices na fun��o objetiva M (II), temos que:

V�rtice	Valor de M
A(0,0)	0
B(0,1500)	6000
C(250,1500)	8000
D(500,1250)	9000
E(1000,500)	10000
F(1000,0)	8000

Como se v�, o maior ganho poss�vel � de R$ 10000,00 ou o que equivale dizer x=1000 e y=500
Ent�o, a solu��o otimizada � dada por:
1) o investidor deve comprar 1000 a��es do tipo 1
2) o investidor deve comprar 500 a��es do tipo 2

Esses dois pequenos exemplos nos mostram como � importante a resolu��o de sistemas lineares na vida pr�tica. Entretanto, problemas mais complexos de programa��o linear s�o resolvidos por uma m�todo chamado "Simplex", com o aux�lio de computadores, j� que a solu��o gr�fica torna-se impratic�vel.